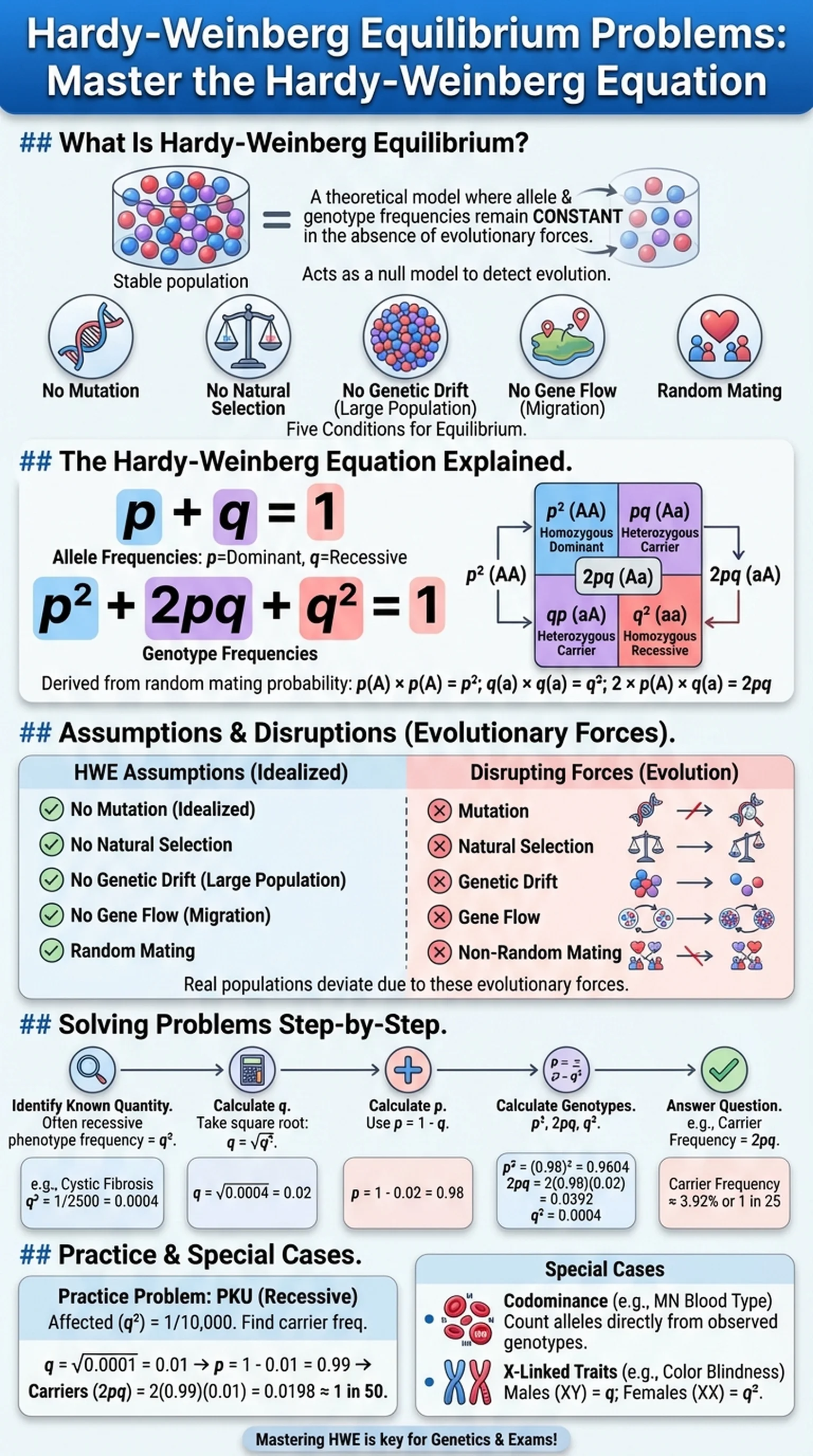
Hardy-Weinberg Equilibrium Problems: Master the Hardy-Weinberg Equation

Hardy-Weinberg equilibrium is a foundational principle of population genetics that describes a theoretical population in which allele frequencies and genotype frequencies remain constant from generation to generation in the absence of evolutionary influences. Independently derived by mathematician G. H. Hardy and physician Wilhelm Weinberg in 1908, the Hardy-Weinberg equilibrium provides a null model against which real populations can be compared to detect the action of evolutionary forces.

In a population at Hardy-Weinberg equilibrium, five conditions must be met: no mutation, no natural selection, no genetic drift (infinitely large population size), no gene flow (migration), and random mating. When all five assumptions hold, the allele frequency of every gene in the population remains unchanged across generations, and genotype frequencies can be predicted directly from allele frequencies using the Hardy-Weinberg equation.

The practical importance of Hardy-Weinberg equilibrium lies in its role as a benchmark. By comparing observed genotype frequencies in a real population to those expected under equilibrium, geneticists can infer which evolutionary forces are at work. If a population deviates significantly from Hardy-Weinberg expectations, at least one of the five assumptions is being violated—perhaps natural selection is favoring one allele, or genetic drift is causing random fluctuations in a small population, or non-random mating is altering genotype proportions.

For medical genetics, Hardy-Weinberg equilibrium is used routinely to estimate carrier frequencies for autosomal recessive disorders. If one in 10,000 individuals is affected (genotype frequency q² = 1/10,000), the allele frequency q = 1/100 and the carrier frequency 2pq ≈ 2/100, or approximately 2% of the population. This calculation is frequently tested on the MCAT and USMLE and is a standard tool in genetic counseling.

Mastering Hardy-Weinberg equilibrium problems begins with understanding the conceptual foundation: a population in equilibrium is not evolving, and any departure from equilibrium signals the presence of one or more evolutionary mechanisms driving changes in allele frequency.

The Hardy-Weinberg equation is the mathematical expression of Hardy-Weinberg equilibrium for a single gene with two alleles. It consists of two related equations that connect allele frequencies to genotype frequencies.

The allele frequency equation is simply p + q = 1, where p represents the frequency of the dominant allele (A) and q represents the frequency of the recessive allele (a). Because there are only two alleles for this locus, their frequencies must sum to one.

The genotype frequency equation is derived by expanding the binomial: p² + 2pq + q² = 1. Here, p² is the expected frequency of the homozygous dominant genotype (AA), 2pq is the expected frequency of the heterozygous genotype (Aa), and q² is the expected frequency of the homozygous recessive genotype (aa). This equation predicts the distribution of genotypes in a population at equilibrium, given the allele frequencies.

The derivation is straightforward. If mating is random, the probability that an offspring receives allele A from one parent is p, and the probability of receiving A from the other parent is also p, so the probability of genotype AA is p × p = p². Similarly, aa has probability q². The heterozygote Aa can arise in two ways—A from parent 1 and a from parent 2 (probability pq), or a from parent 1 and A from parent 2 (probability qp)—giving a total of 2pq.

To apply the Hardy-Weinberg equation to real problems, you typically start with one known quantity. In many Hardy-Weinberg equilibrium problems, you are given the frequency of the recessive phenotype (which equals q² because homozygous recessive individuals are phenotypically distinguishable). From q² you calculate q by taking the square root, then p = 1 - q, and finally 2pq gives the carrier frequency. This stepwise approach works for any autosomal locus with complete dominance.

For loci with codominance or incomplete dominance—such as the MN blood group system—all three genotype frequencies can be observed directly, and the Hardy-Weinberg equation can be tested by comparing observed and expected frequencies using a chi-square goodness-of-fit test. A statistically significant deviation indicates that the population is not in Hardy-Weinberg equilibrium at that locus.

The Hardy-Weinberg equation extends to loci with more than two alleles. For three alleles (p + q + r = 1), the genotype frequencies are given by (p + q + r)² = p² + q² + r² + 2pq + 2pr + 2qr = 1. The ABO blood group system, with alleles I^A, I^B, and i, is a classic example used in population genetics courses.

The Hardy-Weinberg equilibrium rests on five key assumptions. Understanding each assumption is critical not only for solving Hardy-Weinberg equilibrium problems but also for appreciating why real populations almost always deviate from the model. Each violated assumption corresponds to a specific evolutionary mechanism.

The first assumption is no mutation. Mutation introduces new alleles or converts one allele to another, changing allele frequency over time. While mutation rates for individual genes are typically very low (on the order of 10^-5 to 10^-9 per base pair per generation), mutation is the ultimate source of all genetic variation. In practice, mutation alone changes allele frequency so slowly that it rarely causes detectable deviations from Hardy-Weinberg equilibrium in a single generation, but over evolutionary timescales it is indispensable.

The second assumption is no natural selection. Natural selection occurs when individuals with certain genotypes have higher fitness (survival and reproductive success) than others. Directional selection favors one allele over another, changing allele frequency in a consistent direction. Balancing selection (e.g., heterozygote advantage, as in sickle cell trait conferring malaria resistance) maintains multiple alleles in the population. Disruptive selection favors extreme phenotypes. Any form of selection violates Hardy-Weinberg equilibrium by systematically altering allele frequency.

The third assumption is infinitely large population size (no genetic drift). In finite populations, random sampling of gametes from one generation to the next causes stochastic fluctuations in allele frequency called genetic drift. Drift is most powerful in small populations, where it can rapidly fix or eliminate alleles regardless of their fitness effects. The founder effect and population bottlenecks are special cases of drift that can dramatically alter allele frequency in a single event.

The fourth assumption is no gene flow (migration). Gene flow is the transfer of alleles between populations through the movement of individuals or gametes. Immigration introduces new alleles or changes the frequency of existing alleles, while emigration removes alleles. Gene flow tends to homogenize allele frequencies among connected populations.

The fifth assumption is random mating. Non-random mating—including assortative mating (mating with similar phenotypes), disassortative mating, consanguinity (inbreeding), and sexual selection—alters genotype frequencies without directly changing allele frequencies. Inbreeding, for example, increases homozygosity at the expense of heterozygosity, causing a departure from Hardy-Weinberg genotype proportions even though allele frequencies remain unchanged. Understanding these five assumptions is the key to interpreting population genetics data and solving Hardy-Weinberg equilibrium problems on exams.

Hardy-Weinberg equilibrium problems appear on virtually every major biology and medical exam. The key to solving them efficiently is a systematic approach. Here is a step-by-step framework that works for the most common problem types.

Step 1: Identify the known quantity. Most problems provide either the frequency of the recessive phenotype, the frequency of the dominant phenotype, or a specific allele frequency. For autosomal recessive traits, the recessive phenotype frequency equals q². For example, if a problem states that 1 in 2,500 individuals has cystic fibrosis, then q² = 1/2,500 = 0.0004.

Step 2: Calculate q. Take the square root of q². In our example, q = sqrt(0.0004) = 0.02. This is the frequency of the recessive allele (the CFTR mutation allele, in this case).

Step 3: Calculate p. Since p + q = 1, then p = 1 - q = 1 - 0.02 = 0.98. This is the frequency of the dominant (normal) allele.

Step 4: Calculate genotype frequencies. Using the Hardy-Weinberg equation: p² = (0.98)² = 0.9604 (homozygous dominant, unaffected non-carriers), 2pq = 2(0.98)(0.02) = 0.0392 (heterozygous carriers), and q² = 0.0004 (homozygous recessive, affected individuals). Note that the carrier frequency (2pq ≈ 3.92%) is much higher than the affected frequency (0.04%), a clinically important insight.

Step 5: Answer the specific question. If asked for the carrier frequency, report 2pq = 0.0392 or approximately 1 in 25. If asked for the number of carriers in a population of 100,000, multiply: 0.0392 × 100,000 = 3,920 carriers.

For problems involving codominant alleles, the approach is slightly different. If you can directly observe the frequency of each genotype (as with MN blood types), count alleles directly: p = (2 × number of MM + number of MN) / (2 × total individuals), and q = 1 - p.

For X-linked traits, remember that males are hemizygous. The frequency of affected males equals q (not q²), while the frequency of affected females equals q². If 8% of males are color-blind (q = 0.08), the frequency of color-blind females is q² = 0.0064 or 0.64%.

Common pitfalls in Hardy-Weinberg equilibrium problems include confusing phenotype frequency with allele frequency, forgetting to take the square root of q², and assuming dominant phenotype frequency equals p² (it actually equals p² + 2pq). Practice with a variety of problem types will build the fluency needed for exam success.

Working through practice problems is the most effective way to build confidence with the Hardy-Weinberg equation. Below are three representative problems with detailed solutions covering different scenarios commonly encountered in population genetics courses and on standardized exams.

Problem 1: Phenylketonuria (PKU) is an autosomal recessive metabolic disorder. In a certain population, 1 in 10,000 newborns is affected. Assuming Hardy-Weinberg equilibrium, what is the carrier frequency?

Solution: The affected frequency is q² = 1/10,000 = 0.0001. Taking the square root, q = 0.01. Then p = 1 - 0.01 = 0.99. The carrier frequency is 2pq = 2(0.99)(0.01) = 0.0198, or approximately 1 in 50 individuals. This means that for every affected individual, there are roughly 200 carriers in the population—a ratio that underscores the hidden reservoir of recessive alleles in heterozygous form.

Problem 2: In a population of 500 individuals, 320 have blood type M (genotype MM), 160 have blood type MN (genotype MN), and 20 have blood type N (genotype NN). Is this population in Hardy-Weinberg equilibrium?

Solution: Calculate allele frequencies directly. The number of M alleles = 2(320) + 160 = 800. The number of N alleles = 2(20) + 160 = 200. Total alleles = 2(500) = 1,000. So p(M) = 800/1,000 = 0.80 and q(N) = 200/1,000 = 0.20. Expected genotype frequencies: p² = 0.64 (expected MM = 320), 2pq = 0.32 (expected MN = 160), q² = 0.04 (expected NN = 20). Comparing observed to expected: MM observed = 320, expected = 320; MN observed = 160, expected = 160; NN observed = 20, expected = 20. The observed values match expected values perfectly, so this population is in Hardy-Weinberg equilibrium at the MN locus.

Problem 3: Red-green color blindness is X-linked recessive. If 7% of males in a population are color-blind, what percentage of females are expected to be color-blind? What percentage of females are carriers?

Solution: For X-linked traits, the allele frequency q equals the frequency of affected males, so q = 0.07 and p = 0.93. The frequency of color-blind females (homozygous recessive, X^a X^a) = q² = (0.07)² = 0.0049 or 0.49%. The frequency of carrier females (heterozygous, X^A X^a) = 2pq = 2(0.93)(0.07) = 0.1302 or 13.02%. Notice the large difference between male and female affected frequencies, which is a hallmark of X-linked recessive inheritance and a frequent topic in population genetics exams.

These problems illustrate the versatility of the Hardy-Weinberg equation. Whether you are calculating carrier frequencies for genetic counseling, testing equilibrium with codominant markers, or analyzing X-linked traits, the same fundamental allele frequency principles apply.

Real populations are never perfectly at Hardy-Weinberg equilibrium because the five assumptions are idealized conditions that no natural population fully meets. Each violation represents a distinct evolutionary force that changes allele frequency or genotype proportions, driving evolution.

Natural selection is the most directed force. When one genotype confers higher fitness—greater probability of survival and reproduction—its allele frequency increases over generations. Classic examples include the sickle cell allele (HbS) in malaria-endemic regions: heterozygous carriers (HbA/HbS) have a survival advantage over both homozygous genotypes, a phenomenon called heterozygote advantage or overdominance. This balancing selection maintains the HbS allele at an intermediate allele frequency (up to 20% in some West African populations) despite the severe disease caused by homozygosity. For Hardy-Weinberg equilibrium problems that involve selection, you must account for differential fitness by applying selection coefficients to the standard equation.

Genetic drift is the random change in allele frequency due to sampling error in finite populations. In small populations, drift can cause alleles to become fixed (frequency = 1) or lost (frequency = 0) regardless of their selective value. The founder effect occurs when a small group colonizes a new area, carrying only a sample of the original population's allele frequencies. The Amish community's high frequency of Ellis-van Creveld syndrome (a rare recessive condition) is a textbook example of the founder effect altering allele frequency.

Gene flow counteracts differentiation between populations. When individuals migrate between populations and reproduce, they introduce alleles that may be at different frequencies in the source population. Over time, gene flow tends to homogenize allele frequencies across connected populations, reducing genetic divergence. In conservation biology, managed gene flow (translocation of individuals) is used to rescue small, inbred populations from the deleterious effects of drift.

Mutation provides the raw material for evolution by generating new alleles. Although mutation rates per locus are low, the cumulative effect across the entire genome is substantial. Mutation-selection balance describes the equilibrium between the introduction of deleterious alleles by mutation and their removal by natural selection, maintaining disease alleles at low but non-zero frequencies in the population.

Non-random mating, including inbreeding and assortative mating, alters genotype frequencies without changing allele frequencies. Inbreeding increases homozygosity, which exposes deleterious recessive alleles and can lead to inbreeding depression—reduced fitness in inbred offspring. Populations that practice consanguineous marriage show elevated frequencies of autosomal recessive disorders, a pattern detectable as deviation from Hardy-Weinberg equilibrium at disease-associated loci.

For students of population genetics, understanding these evolutionary forces is as important as mastering the Hardy-Weinberg equation itself. Exams frequently present scenarios and ask you to identify which force is responsible for a given deviation from equilibrium. Building a mental checklist of the five assumptions and their corresponding violations will serve you well on any Hardy-Weinberg equilibrium problems you encounter.