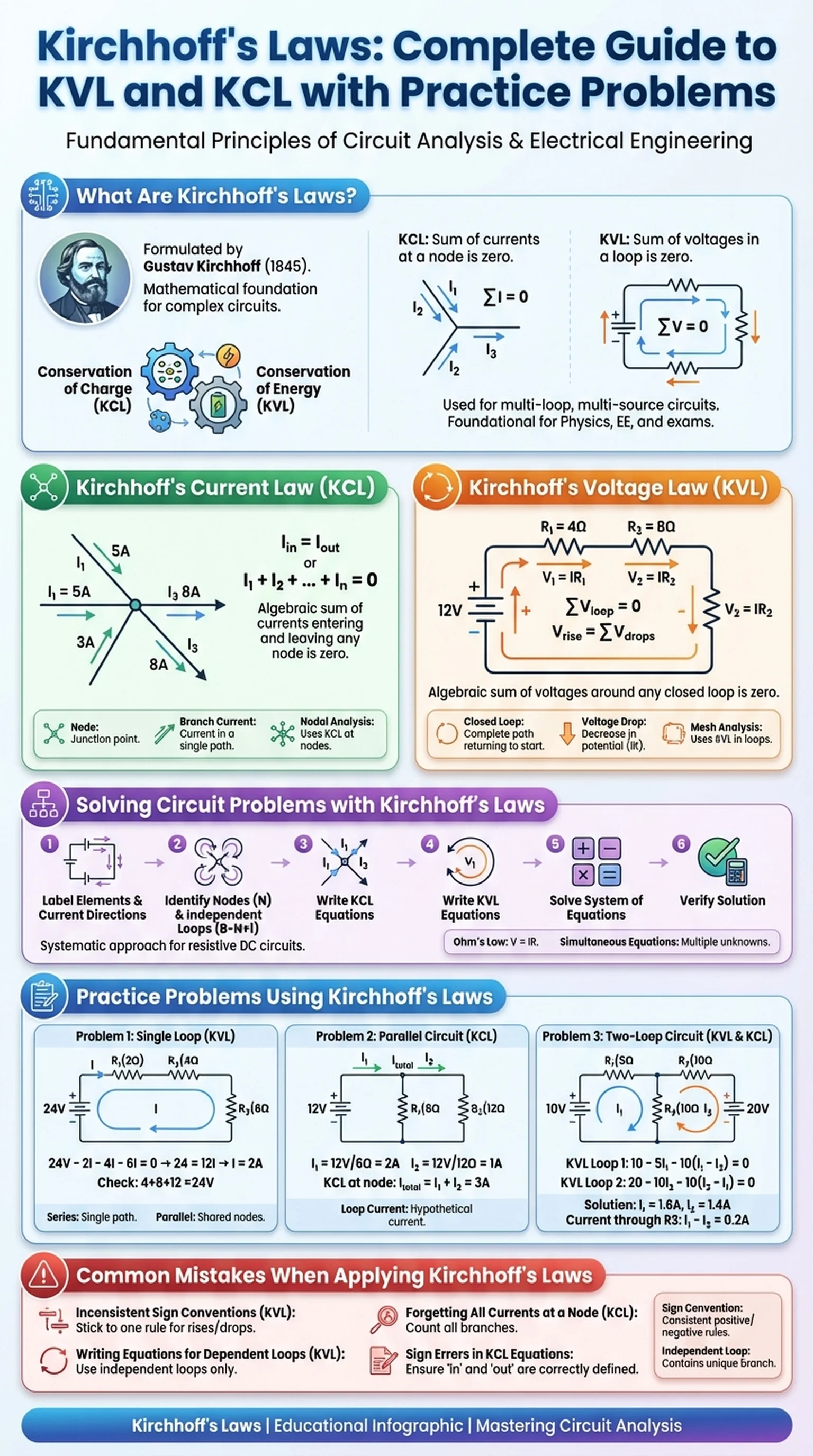
Kirchhoff's Laws: Complete Guide to KVL and KCL with Practice Problems

Kirchhoff's laws are two fundamental principles of electrical circuit analysis formulated by German physicist Gustav Kirchhoff in 1845. These laws — Kirchhoff's current law (KCL) and Kirchhoff's voltage law (KVL) — provide the mathematical foundation for analyzing any electrical circuit, no matter how complex. Together, they allow engineers and physics students to determine unknown currents, voltages, and resistances in circuits that cannot be simplified using series and parallel rules alone.

Kirchhoff's laws are built upon two conservation principles from physics. KCL is based on the conservation of electric charge, which states that charge cannot be created or destroyed. KVL is based on the conservation of energy, which states that the total energy gained by a charge traveling around a closed loop must equal the total energy lost. These conservation laws are among the most fundamental in all of physics, which is why Kirchhoff's laws have remained indispensable for over 175 years.

In practice, Kirchhoff's laws are essential for analyzing circuits that contain multiple loops, multiple sources, or combinations of components that do not reduce neatly into series or parallel configurations. While Ohm's law relates voltage, current, and resistance for a single component, Kirchhoff's laws provide the system of equations needed to solve for all unknowns in a multi-component circuit. They are foundational topics in introductory physics courses, electrical engineering programs, and standardized exams including the FE exam, the AP Physics exam, and the MCAT.

In the following sections, we will explore each of Kirchhoff's laws in detail, work through step-by-step examples of circuit analysis, and provide practice problems to help you master these essential tools. Whether you are a physics student encountering circuits for the first time or an engineering student preparing for professional licensure, a solid command of KCL and KVL will serve you throughout your career.

Kirchhoff's current law, often abbreviated as KCL, states that the algebraic sum of all currents entering and leaving any node (junction) in a circuit is zero. Equivalently, the total current flowing into a node must equal the total current flowing out of that node. This law is a direct consequence of the conservation of electric charge: since charge cannot accumulate at a single point in a circuit under steady-state conditions, whatever flows in must flow out.

Mathematically, KCL is expressed as the summation of currents at a node equals zero. If we define currents entering a node as positive and currents leaving as negative (or vice versa, as long as the convention is consistent), the equation becomes: I1 + I2 + I3 + ... + In = 0. For example, if three wires meet at a node and 5 A flows in through wire one, 3 A flows in through wire two, then 8 A must flow out through wire three, since 5 + 3 - 8 = 0.

KCL applies at every node in a circuit, and each node provides one equation. For a circuit with N nodes, KCL provides N-1 independent equations (one node serves as the reference). These equations, combined with component equations from Ohm's law and the equations from Kirchhoff's voltage law, form the complete system needed to solve for all unknown quantities.

KCL is particularly useful for analyzing parallel circuits and circuits with multiple branches. When components are connected in parallel, they share the same two nodes, and KCL at either node immediately relates the branch currents to the total current. In more complex topologies, KCL at each junction constrains the possible current distributions and is essential for techniques like nodal analysis, which uses KCL as its primary tool.

A common mistake students make with Kirchhoff's current law is forgetting to account for all currents at a node, including those through components like capacitors or inductors in AC circuits. In DC steady-state analysis, capacitors act as open circuits and inductors act as short circuits, simplifying the application of KCL. However, in AC or transient analysis, all branch currents must be included. Consistent practice with KCL builds the intuition needed to handle circuits of any complexity.

Kirchhoff's voltage law, abbreviated as KVL, states that the algebraic sum of all voltages around any closed loop in a circuit is zero. In other words, if you start at any point in a circuit and trace a path that returns to the starting point, the sum of all voltage rises (from sources) and voltage drops (across resistors and other components) will equal zero. This law is a direct consequence of the conservation of energy: a unit of charge traveling around a complete loop must return with the same energy it started with.

Mathematically, KVL is expressed as the summation of voltages around a loop equals zero. Convention dictates that voltage rises (such as traversing a battery from negative to positive terminal) are positive, while voltage drops (such as traversing a resistor in the direction of current flow) are negative. Applying Ohm's law, the voltage drop across a resistor R carrying current I is IR, and this term appears with a negative sign in the KVL equation when the traversal direction matches the current direction.

Consider a simple series circuit with a 12 V battery and two resistors, R1 = 4 ohms and R2 = 8 ohms, connected in a single loop. By Kirchhoff's voltage law: +12 V - I(4) - I(8) = 0. Solving for I gives 12 = 12I, so I = 1 A. The voltage drops across R1 and R2 are 4 V and 8 V, respectively, and their sum equals the 12 V source — confirming KVL.

For circuits with multiple loops, KVL provides one equation per independent loop. The number of independent loops in a circuit equals the number of branches minus the number of nodes plus one (B - N + 1). Mesh analysis, a powerful circuit analysis technique taught in electrical engineering courses, is built entirely on Kirchhoff's voltage law. In mesh analysis, you assign a loop current to each independent loop, write KVL for each loop using Ohm's law, and solve the resulting system of equations.

KVL also applies to circuits containing dependent sources, capacitors, and inductors, though the voltage expressions for these components differ from simple resistors. For capacitors, V = Q/C, and for inductors, V = L(dI/dt). Regardless of the component type, the fundamental principle of Kirchhoff's voltage law remains the same: the sum of all voltage changes around any closed loop is zero.

Solving circuit problems using Kirchhoff's laws requires a systematic approach that combines KCL, KVL, and Ohm's law into a coherent framework. The following step-by-step method works for any resistive DC circuit and extends naturally to more complex scenarios.

Step one is to label all circuit elements and assign current directions. Choose a direction for the current through each branch. If your assumed direction is wrong, the math will yield a negative value for that current, which simply means the actual direction is opposite to your assumption. Label all resistor values and source voltages.

Step two is to identify nodes and loops. Count the number of nodes (N) and the number of independent loops (B - N + 1, where B is the number of branches). You will write N-1 KCL equations and enough KVL equations to reach the total number of unknowns.

Step three is to write KCL equations at each node except one. At each node, set the sum of currents entering equal to the sum of currents leaving. For example, at a node where currents I1 and I2 enter and I3 leaves: I1 + I2 = I3.

Step four is to write KVL equations for each independent loop. Traverse each loop in a consistent direction (clockwise or counterclockwise) and sum all voltage rises and drops. Apply Ohm's law to express voltage drops across resistors as the product of current and resistance. For example, in a loop containing a 10 V battery and resistors of 2 ohms and 3 ohms: 10 - 2I1 - 3I2 = 0.

Step five is to solve the system of equations. You now have a set of simultaneous linear equations with currents as unknowns. Use substitution, elimination, or matrix methods to solve. For circuits with three or more unknowns, organizing the equations in matrix form and using Cramer's rule or Gaussian elimination is often the most efficient approach.

Step six is to verify your solution. Plug the solved current values back into both the KCL and KVL equations to confirm they are satisfied. Also check that power delivered by sources equals power consumed by resistors (conservation of energy check). This verification step is crucial for exam settings where partial credit may depend on demonstrating a correct methodology.

Applying Kirchhoff's laws consistently using this method will allow you to solve any resistive DC circuit. With practice, you will develop the ability to identify the most efficient combination of KCL and KVL equations for each circuit topology.

The following practice problems are designed to build your proficiency with Kirchhoff's current law and Kirchhoff's voltage law across a range of circuit configurations. Work through each problem on paper before checking the solution.

Problem 1 (Single Loop — KVL Only): A circuit contains a 24 V battery in series with three resistors: R1 = 2 ohms, R2 = 4 ohms, and R3 = 6 ohms. Find the current and the voltage across each resistor. Solution: By KVL around the single loop: 24 - 2I - 4I - 6I = 0, so 24 = 12I, giving I = 2 A. Voltage drops: V1 = 2(2) = 4 V, V2 = 4(2) = 8 V, V3 = 6(2) = 12 V. Check: 4 + 8 + 12 = 24 V, confirming KVL.

Problem 2 (Parallel Circuit — KCL): A 12 V battery is connected to two resistors in parallel: R1 = 6 ohms and R2 = 12 ohms. Find the current through each resistor and the total current. Solution: By Ohm's law, I1 = 12/6 = 2 A and I2 = 12/12 = 1 A. By KCL at the node where the branches meet: I_total = I1 + I2 = 3 A. Total resistance = 12/3 = 4 ohms, consistent with the parallel formula.

Problem 3 (Two-Loop Circuit — KVL and KCL): A circuit has two loops sharing a common branch. Loop 1 contains a 10 V battery, R1 = 5 ohms, and a shared R3 = 10 ohms. Loop 2 contains a 20 V battery, R2 = 10 ohms, and the shared R3 = 10 ohms. Assign loop currents I1 (clockwise in loop 1) and I2 (clockwise in loop 2). KVL for loop 1: 10 - 5I1 - 10(I1 - I2) = 0, giving 10 = 15I1 - 10I2. KVL for loop 2: 20 - 10I2 - 10(I2 - I1) = 0, giving 20 = -10I1 + 20I2. Solving the system: from equation 1, I1 = (10 + 10I2)/15. Substituting into equation 2 and solving yields I2 = 1.4 A and I1 = 1.6 A. The current through R3 is I1 - I2 = 0.2 A.

These practice problems demonstrate the application of Kirchhoff's laws to progressively more complex circuits. Mastering multi-loop problems like Problem 3 is the key skill developed by studying KCL and KVL together, and it forms the foundation for advanced circuit analysis in engineering courses.

Students frequently encounter pitfalls when first learning to apply Kirchhoff's laws to circuit problems. Being aware of these common mistakes can save significant time and frustration during homework, lab work, and examinations.

The most prevalent mistake with Kirchhoff's voltage law is inconsistent sign conventions. When traversing a loop, you must maintain the same convention throughout: if you define a voltage rise as positive and a voltage drop as negative, you must apply this consistently to every element in the loop. A frequent error is assigning the wrong sign to a battery — remember that traversing a battery from its negative to its positive terminal is a voltage rise, while going from positive to negative is a voltage drop, regardless of the current direction.

Another common KVL error is writing equations for dependent loops instead of independent loops. If a circuit has three loops but only two are independent, writing all three KVL equations produces a redundant system. The number of independent KVL equations equals B - N + 1. Using extra equations will not cause an incorrect answer, but it wastes time and can introduce arithmetic errors.

For Kirchhoff's current law, the most common mistake is forgetting to include all currents at a node. Students sometimes overlook a branch that connects to the node, especially in complex circuit diagrams. Before writing the KCL equation, count the total number of branches meeting at the node and ensure each one appears in the equation.

Sign errors in KCL equations also cause problems. If you define all currents entering a node as positive, then all currents leaving must be negative. Mixing conventions within a single equation produces incorrect results. Some students find it easier to use the form "currents in = currents out" rather than "sum of all currents = 0" to reduce sign confusion.

Arithmetic errors when solving simultaneous equations are another major source of mistakes, particularly in multi-loop problems. Double-check your algebra, especially when multiplying equations by scaling factors to eliminate variables. Using matrix methods or a calculator for the algebra portion can help reduce these errors.

Finally, students sometimes forget to verify their solution. After solving for all currents, plug the values back into every KCL and KVL equation to confirm they balance. Also verify that the power delivered by all sources equals the power dissipated by all resistors. This verification step is the hallmark of thorough circuit analysis using Kirchhoff's laws and builds confidence that your solution is correct.